PythagoraS

Sejarah dan penjelasan lengkap mengenai teorema Pythagoras

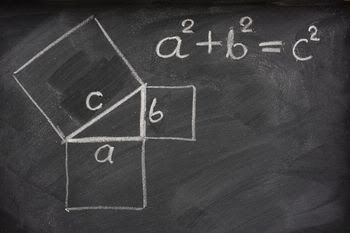
Phytagoras adalah pembelajaran mengenai segitiga siku-siku yang menyatakan bahwa kuadrat dari sisi miring adalah sama dengan jumlah kuadrat dari sisi-sisi siku-sikunya.
contoh segitiga siku-siku :

ecara matematis rumus Phytagoras ini ditulis :
a^2 + c^2 = b^2
dimana a dan c adalah sisi siku-siku, sedangkan b adalah sisi miringnya
Contoh soal Pythagoras :
Contoh soal:



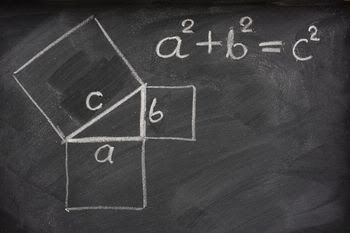
Jika panjang a = 4 cm, dan panjang b = 3 cm.. maka berapakah panjang c?

Rumusnya: a^2 + b^2 = c^2
4^2 + 3^2 = c^2
16 + 9 = c^2
25 = c^2
c = v25
c = 5

maka, panjang c adalah 5 cm

Phytagoras, penemu teorema ini



Phytagoras (Lahir tahun 570 SM sampai kematiannya pada tahun 495 SM) adalah seorang matematikawan dan filsuf Yunani yang paling dikenal melalui teoremanya.
Dikenal sebagai "Bapak Bilangan", dia memberikan sumbangan yang penting terhadap filsafat dan ajaran keagamaan pada akhir abad ke-6 SM.

Yap, teorema ini diambil oleh peninggalnya, Phytagoras namun nyatanya fakta-fakta teori ini pertama kali diketahui oleh matematikawan Cina dan Mesir jauh sebelum Phytagoras lahir. Lalu mengapa nama filsuf yunani ini diabadikan ke Teori yang sudah dikenal masyarakat bertahun-tahun sebelum dia lahir?

Arstitek Mesir sering menggunakan 3,4,5 segitiga siku-siku (segitiga siku-siku dengan 12 ikatan) sebagai alat praktis dalam membuat bujur sangkar dan palang arsitektur mesir

3,4,5 segitiga siku-siku:

Untuk Mesir, tidak hanya angka-angka ganjil dan genap-mereka adalah laki-laki dan perempuan. Setiap bagian dari alam semesta itu / adalah seorang laki-laki atau perempuan. Tidak ada netral (benda). Tidak seperti di Inggris, di mana ada she, he, atau it, di Mesir hanya ada she dan he.

Angka animasi ini di Mesir Kuno yang disebut oleh Plutarch, di Moralia Vol V, ketika ia menggambarkan 3-4-5 Mesir segitiga:

Yang lurus keatas dapat disamakan dengan laki-laki, pangkalan ke betina, dan sisi miring adalah anak kedua, dan begitu Ausar [Osiris] dapat dianggap sebagai asal-usul, Auset [Isis] sebagai penerima, dan Heru [Horus] sebagai hasil sempurna. Tiga adalah angka ganjil pertama yang sempurna: empat adalah sisi persegi yang bahkan adalah nomor dua, tetapi lima ini dalam beberapa hal seperti kepada ayah, dan dalam beberapa hal seperti untuk ibunya, yang terdiri atas tiga dan dua. Dan panta [semua] adalah turunan dari pente [lima], dan mereka berbicara tentang penghitungan sebagai "penomoran oleh balita". Lima membuat persegi dengan sendirinya.

Catatan Cina tertua mengenai Teorema phytagoras dikenal dengan nama Teorema Shang Gao, dan dinamai oleh Astrolog Adipati Zhou, dan dijelaskan dalam koleksi matematika Chou Pei Suan Ching. Dan di India, teorema ini dikenal sebagai Teorema Bhaskara.

Chou Pei Suan Ching:
Bukti visual tentang 3,4,5 segitiga yang ada di Chou Pei Suan Ching 500-200 SM

Selain bangsa cina, mesir, bahkan India, teori segitiga siku-siku ini juga sudah diketahui oleh bangsa Babilonia dan masyarakat eropa utara. Tetapi mereka hanya menggunakan pengetahuan ini dalam kehidupan sehari-hari, tidak bisa membuktikan teorinya . Tetapi, Phytagoras seorang yang gigih dan pantang menyerah. Kemudian, dialah orang yang pertama kali membuktikan teori Phytagoras bahwa jumlah hasil kuadrat dari kedua sisi siku-siku sama dengan kuadrat dari sisi miringnya . Dia berhasil membuktikanya dengan luas bujur sangkar untuk menghubungkan ketiga sisi tersebut

Teorema Phytagoras

Teorema ini bisa digunakan pada setiap segitiga siku-siku. Segitiga siku-siku adalah segitiga yang memiliki sudut siku-siku, dan sudut siku-siku merupakan sudut 90derajat .

Contoh segitiga siku-siku saat dimiringkan :

Setelah melihat gambar diatas, apa yang ada di pikiran agan ? menurut agan gambar diatas itu apa ?

Jika segitiga phytagoras menyatakan kuadrat dari kedua sisi siku-siku sama dengan kuadrat sisi miringnya, bagaikan celana dalam.. dimana paha atas adalah kuadrat sisi siku-siku dan badannya adalah kuadrat dari sisi miringnya

phytagoras:


Bukti bahwa jumlah luas persegi dari sisi miring segitiga siku-siku sama dengan jumlah persegi dari sisi lainnya bisa bedasarkan gambar diatas. Bayangkan aja agan mempunyai ubin segitiga berwarna merah yang merupakan celana dalam aka segitiga siku-siku.. dan buatkan persegi disetiap sisi siku-sikunya (2 sisi yang membentuk V) dengan 2 ubin segitiga. Dan buatkan juga persegi di sisi satunya lagi dengan 4 ubin segitiga.

Maka :
2 ubin segitiga + 2 ubin segitiga = 4 ubin segitiga

Hal ini bisa membuktikan bahwa jumlah kuadrat dari segitiga siku-siku sama dengan kuadrat dari sisi miringnya